The Golden Rectangle
Benzoic Acid Melt Crystal 2006-036, ©2006 Doug Craft
Mancos Shale, Utah, 2004-036, ©2006 Doug Craft
Golden Ratio Forms for Art by Doug Craft |
| Reload Page in Frames | Artist Info | Email Doug | Home/Artwork |
While my earlier collages were figurative with a clear visual distinction between foreground objects and background, my abstract work since 1997 has been exploring a new concept that I call The Collage of Backgrounds. This technique basically arranges natural abstract images - what would be considered backgrounds in my figurative collages - according to simple geometric rules based on Sacred Geometry and the Golden Ratio. Knowledge of the Golden Section, ratio, or proportion has been known for a very long time. The Egyptians knew about it and the Greeks learned about it from them. It is called phi, Φ, in honor of the sculptor Phidias, one of the architects of the Parthenon, and is approximated by the irrational fraction 0.6180339... Φ shows up throughout nature and represents one of the most fundamental numerical constants of the universe. For example, the finger bones are in approximate Φ ratio to each other, and the position of features on the human body is related to Φ.
The square combined with various Golden Rectangles (GRs) represent the fundamental geometric forms used in all my collages and other work, both figurative and abstract. Squares combined with GR's in Golden Ratio proportion can create a wide range of possible Golden proportional rectangles and image aspect ratios. Since 2008, I have also been using the obtuse and acute Golden Triangle as a template for foreground object placement in figurative collages and as collage objects in abstract collages. The following is an explanation and visual guide to the Golden Ratio-derived shapes and geometric forms that I use in my collages, montages, and artwork in other media. I published my detailed aesthetic theory as a chapter in an academic book published in 2012.
The Golden Rectangle |
|
| The Golden Rectangle is one of the fundamental forms I use for all of my artwork. The GR is a rectangle with an aspect ratio of 1 to 1.618..., or 1 to (1+Φ) as seen in the following examples. | |
Benzoic Acid Melt Crystal 2006-036, ©2006 Doug Craft |
Mancos Shale, Utah, 2004-036, ©2006 Doug Craft |
Coiled Golden Rectangles |
|
|
Below we see an interesting property of GR's that inspired one of my basic Collage of Backgrounds forms - the Coiled Golden Rectangle. When you cut out a square starting from one of the short sides of a GR (the gray square in GR #2 below), the square divides the long side at the Golden Ratio, and you will be left with another GR at a 90° counter-clockwise angle (the smaller vertical white GR in #2 on the right). You can continue to cut out short side squares for each successively smaller GR (as in GR #3) and another smaller white GR will remain - once again rotated 90° counter-clockwise. This process may continue leaving a smaller proportional GR as seen in GR #4. 1 |
|
|
Below is a GR subdivided by Golden-proportional squares that converges on a point called the Eye of God - and hence the notion of a Coil. A superimposed logarithmic spiral also converges on this point, as does the intersection of diagonals (red lines, called radicals) from the primary GR, and the 1st subordinate GR.
|
Below is a collage from the Elements in Golden Ratio series. This series of 84 collages explores the classical elements of earth, air, fire, water, and life (the 5th element that combines all 4 basic elements). The GR coils from this series are also used as collage elements in the square root of five and mandala forms, as well as in collage assemblages. AIR: Golden Rectangle Coil 2004-004, © 2004 Doug Craft |
Golden Triangles |
|
|
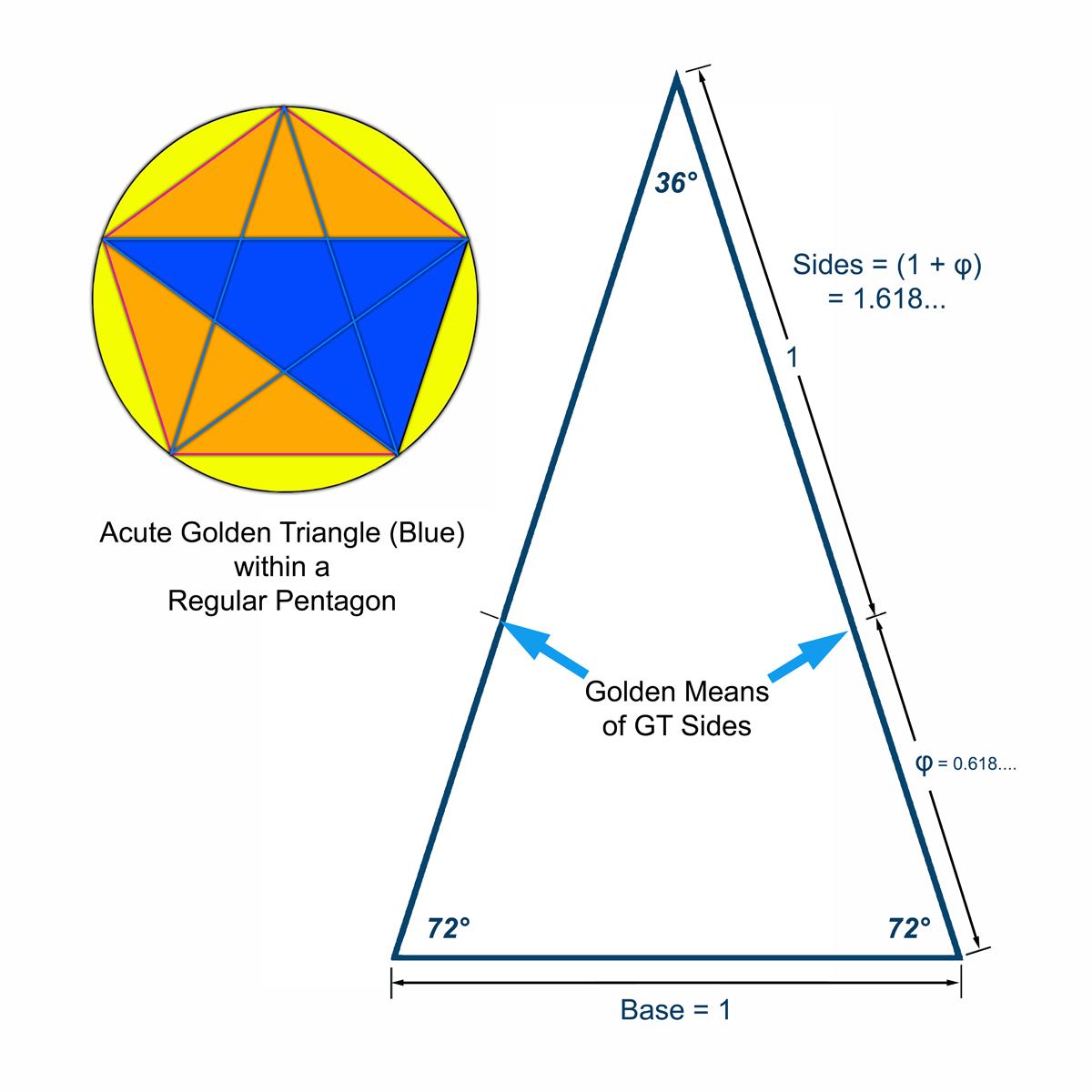
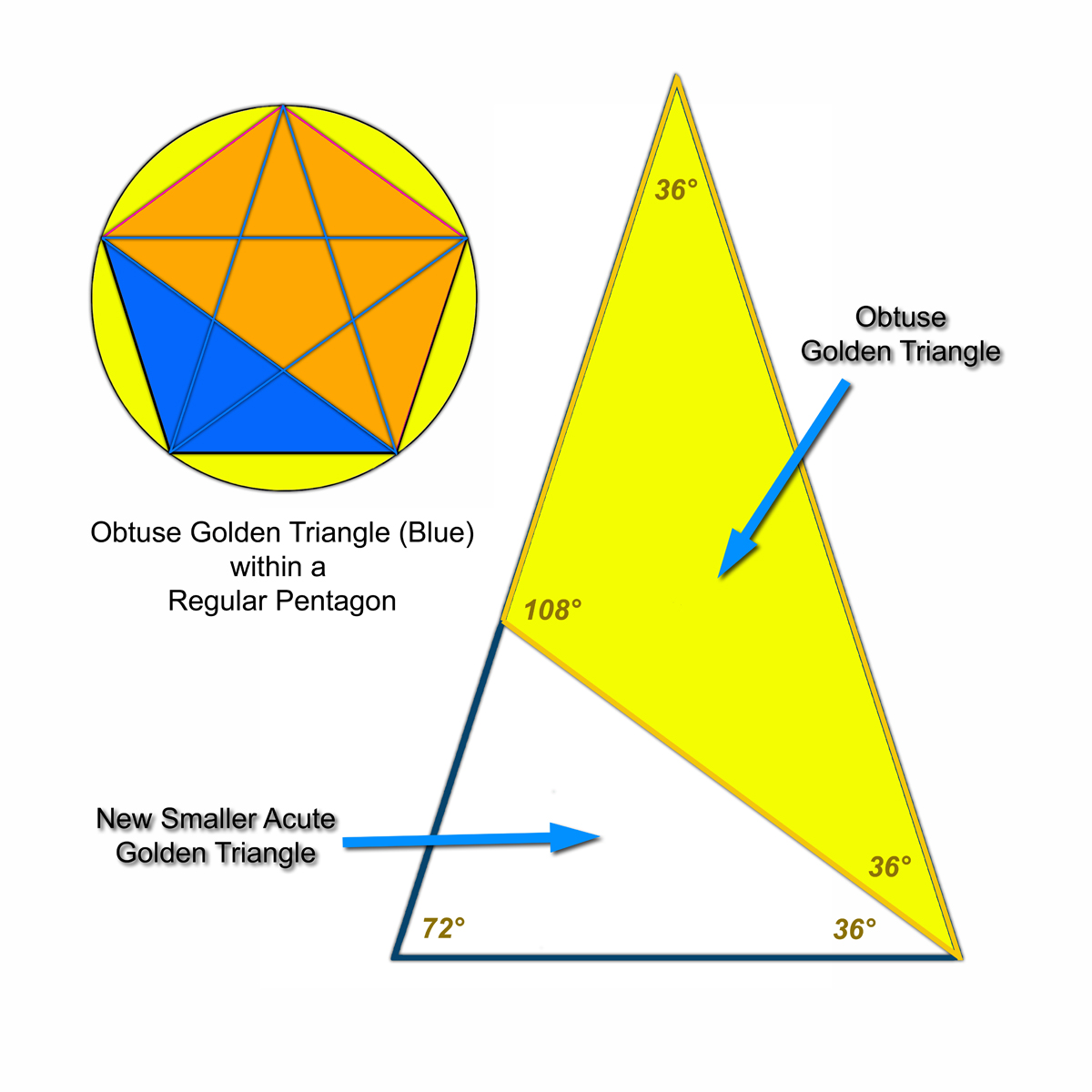
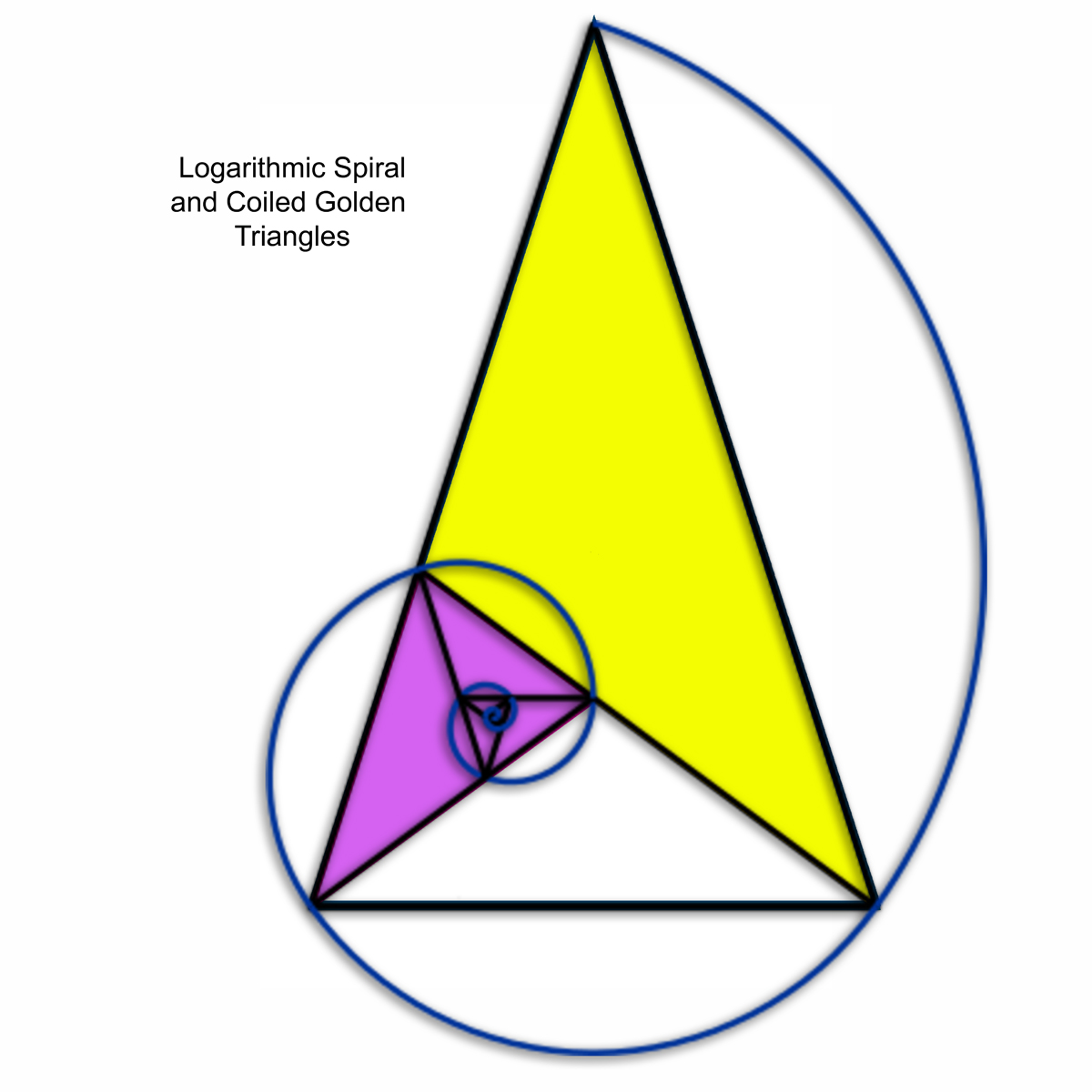
I use the acute and obtuse Golden Triangles in my work to locate foreground objects in the composition and as collage objects. Both of these triangles arise from drawing diagonals within a regular pentagon, as seen in figures 1 and 2 below. The acute GT (figure 1) has a base=1 and sides = (1 + Φ), with base angles of 72° and apex angle of 36°. The Obtuse GT (figure 2) has base angles of 36°, base = (1 + Φ), and apex angle of 108° with sides=1. Like the Golden Rectangle, the GT shows a coiling property created when the acute GT is sectioned at the Golden Mean of the side opposite the base angle, creating a smaller obtuse GT (yellow in figure 2) and another smaller proportional acute GT. Figure 3 shows how a logarithmic spiral can be constructed from continued sectioning of the GT. |
|
Figure 1 - Showing how the acute GT is derived from diagonals within a regular pentagon (left) and that the base is length=1 with sides = (1 + Φ). |
Figure 2 - The obtuse GT is also formed by the diagonals of the regular pentagon (left, in blue). Here we see the first sectioning of the acute GT that creates an obtuse GT (yellow) and a smaller proportional acute GT. |
Figure 3 - Here we see that continued sectioning of the smaller acute GT produces a coiling effect that outlines the logarithmic spiral. |
|
|
|
|
|
B-45s at Failsafe 2012-008, © 2012 Doug Craft |
Test C Tribute 2012-045, © 2012 Doug Craft |
|
|
Golden Triangles 2017-002, ©2017 Doug Craft |
Golden Triangles 2016-023, © 2017 Doug Craft |
The Square-Root of 5 (√5) Ratio and Rectangle |
|
The figure below shows that every GR can coil in 4 different directions and has 4 Eyes of God. The 4 Eyes of God form the vertices of the tan colored GR in the center with sides in 1 to 2.236..., or √5 ratio to the larger GR. On either side of the center GR we see 2 vertical green rectangles - and these have an aspect ratio of 1: 2.236... I call these green rectangles Square Root of 5 Rectangles. |
|
Double Arch, Arches National Park, Utah, |
AIR - Square Root of 5 Collage 2004-003, |
|
|
Square Forms: The Offset Proportional Square and Mandala |
|
|
Below is a form diagram showing a square with three proportionally smaller squares I call an Offset Proportional Square. Each smaller square is in Golden Ratio to the next larger square. |
Below - AIR: Elements Offset Proportional Square 2004-003, a collage of backgrounds combining images of earth, air, fire, and water. I used this particular idea as an organizing form and as a collaged element for other work in the Elements in Golden Ratio series. © 2008 Doug Craft |
The mandala is another of my square forms that uses a central square surrounded by proportional GR's. Mandalas are round or square designs that focus the viewer's attention on the center. As such they are often used as visual meditation objects. Below is the mandala form diagram showing how each of the peripheral GR's shares the same central square, forming four larger overlapping Golden Rectangles. The double square, a form thought sacred by the Egyptians, may also be found in the mandala form diagram. |
Below is an example mandala collage, EARTH: Elements Mandala 2004-004. Note the use of offset proportional squares in the corner positions. © 2008 Doug Craft |
One Plus 3(Φ) Forms |
|
.jpg)
|
Left - These forms are based on a horizontal Golden Rectangle with two proportionally smaller vertical GR's on the ends, or a square with 3 vertical GR's joined together. Proportional diamonds (orange squares rotated 45°) are centered and overlaid on the background rectangle. The aspect ratio of this rectangle is 1 to (1 + 3Φ), or 1 to 2.854... The overlaid diamonds create a bold angular break with the rectangular background. I have called these forms Seals (as in emblems or logos) and created an exploratory series of collages called Seals of the Great Kings using this format. |
|
|
|
 |
|
Double and Triple Golden Rectangles |
|
These wide aspect ratio forms are primarily used when I create panorama images, either traditional landscape panoramas, or triple Golden Rectangle photomontages: |
Lake Powell Inflow, Utah, Double Golden Rectangle Panorama 2003-013, © 2003 Doug Craft |
Microcosmos Number 1, Triple Golden Rectangle Photomontage, 2002-001, © 2002 Doug Craft |
Mount Evans, Colorado, Triple Golden Rectangle Panorama 2003-027, © 2008 Doug Craft |
Tandem Golden Rectangles |
|
A Golden Ratio form used - unknowingly - in my earliest collages was the joining of two vertical GR's in tandem. My collages actually used the 8" x 10" format popular in photographic printing. Only later did I realize this size contained the Golden Ratio by combining two 5" x 8" Fibonacci number GR's. |
Agricultural Suspension, collage, ©1980 Doug Craft |
Email Doug Craft
Reload Navigation Buttons
Doug Craft Fine Art Home
2
3
4
